Mengenal Konsep Bilangan Biner dan Desimal dalam Sistem Digital
Jaringan Sibuk. Sistem bilangan biner merupakan sistem bilangan yang paling banyak digunakan dalam sistem digital karena sistem bilangan ini secara langsung dapat mewakili logika yang ada.
Sistem digital hanya mengenal dua logika, yaitu 0 dan 1.
Logika 0 biasanya mewakili kondisi mati dan logika 1 mewakili kondisi hidup.
Pada sistem bilangan biner, hanya dikenal dua lambang, yaitu 0 dan 1.
Karena itu, sistem bilangan biner paling sering digunakan untuk merepresentasikan kuantitas dan mewakili keadaan dalam sistem digital maupun sistem komputer.
Digit bilangan biner disebut binary digit atau bit.
Empat bit dinamakan nibble dan delapan bit dinamakan byte.
Perbedaan mendasar dari metoda biner dan desimal adalah berkenaan dengan basis.
Jika desimal berbasis 10 (X10) berpangkatkan 10x, maka untuk bilangan biner berbasiskan 2 (X2) menggunakan perpangkatan 2x.
Pada sistem ini, hanya dikenal dua lambang bilangan, yaitu: B = { 0, 1 }.
Ciri suatu bilangan biner adalah adanya tambahan subskrip bin (biner) atau 2 atau tambahan huruf B di akhir bilangan.
Contoh:
1010011bin = 10100112 = 1010011B.
Perhatikan contoh soal pada Gambar 1 di bawah ini!
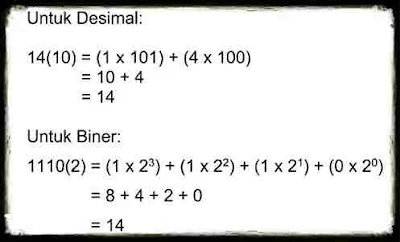 |
| Gambar 1 |
Adapun bentuk umum dari bilangan biner dan bilangan desimal pada Gambar 2 adalah sebagai berikut:
 |
| Gambar 2 |
Sekarang kita balik lagi ke contoh soal di atas (pada Gambar 1)!
Darimana kita dapatkan angka desimal 14(10) menjadi angka biner 1110(2)?
Mari kita lihat lagi pada bentuk umumnya (lihat Gambar 3 di bawah ini)!
 |
| Gambar 3 |
Silahkan lihat dan telusuri perlahan-lahan!
- Pertama sekali, kita jumlahkan angka pada desimal sehingga menjadi 14. anda lihat angka-angka yang menghasilkan angka 14 adalah 8, 4, dan 2!
- Untuk angka-angka yang membentuk angka 14 (lihat angka yang diarsir), diberi tanda biner 1, selebihnya diberi tanda 0. Sehingga kalau dibaca dari kanan, angka desimal 14 akan menjadi 00001110 (terkadang dibaca 1110) pada angka biner-nya.
Mengubah Angka Biner ke Desimal
Perhatikan contoh!
11001101(2)
 |
| Gambar 4 |
Angka desimal 205 didapat dari penjumlahan angka yang di arsir (128+64+8+4+1).
Setiap biner yang bertanda 1 akan dihitung, sementara biner yang bertanda 0 tidak dihitung, alias 0 juga.
Mengubah Angka Desimal ke Biner
Untuk mengubah angka desimal menjadi angka biner digunakan metode pembagian dengan angka 2 sambil memperhatikan sisanya.
Penjumlahan Biner
Penjumlahan biner tidak begitu beda jauh dengan penjumlahan desimal.
Seperti bilangan desimal, bilangan biner juga dijumlahkan dengan cara yang sama.
Pertama-tama yang harus dicermati adalah aturan pasangan digit biner berikut:
0 + 0 = 0
0 + 1 = 1
1 + 1 = 0 dan menyimpan 1
Sebagai catatan, bahwa jumlah dua yang terakhir adalah:
1 + 1 + 1 = 1 dengan menyimpan 1.
Pengurangan Biner
Bentuk Umum pengurangan:
0 - 0 = 0
1 - 0 = 1
1 - 1 = 0
0 - 1 = 1 dengan meminjam 1 dari digit di sebelah kirinya!
Representasi Bilangan Positif dan Negatif pada Bilangan Biner
- Label tanda konvensional : + dan
- Contoh: +4 dan -4
- Menggunakan posisi digit sebelah kiri (MSB) sebagai sign digit (0 untuk positif dan 1 untuk negatif).
- Contoh:
- Sign-Magnitude +9 dalam 8 bit = 00001001
- Sign-Magnitude -4 dalam 4 bit = 1100
Magnitude dari bilangan positif dan negatif sama hanya berbeda pada sign digitnya/ MSB.
Terdapat dua sistem bilangan biner, yaitu bilangan biner tak bertanda dan bilangan biner bertanda.
Pada sistem bilangan biner tak bertanda, hanya dikenal bilangan biner posisif dan tidak diijinkan adanya bilangan biner negatif.
Di sini semua bit digunakan untuk merepresentasikan suatu nilai.
Terdapat dua cara untuk mengubah suatu bilangan positif ke bilangan negatif, yaitu menggunakan sistem bilangan biner komplemen satu dan sistem bilangan biner komplemen dua.
Cara pertama, merupakan cara yang paling mudah ditempuh. Dengan cara ini, untuk mengubah bilangan positif ke negatif cukup dilakukan dengan mengubah bit 0 ke 1 dan bit 1 ke 0 pada setiap bit suatu bilangan biner.
Sebagai contoh, 101101 merupakan bilangan biner dengan nilai 45.
Maka -45 sama dengan 010010.
1 0 1 1 0 1 bilangan biner asli
0 1 0 0 1 0 bilangan biner komplemen satu
Sistem Oktal dan Heksa Desimal
Bilangan oktal adalah bilangan dasar 8, sedangkan bilangan heksadesimal atau sering disingkat menjadi heks. ini adalah bilangan berbasis 16.
Karena oktal dan heks ini merupakan pangkat dari dua, maka mereka memiliki hubungan yang sangat erat.
Oktal dan heksadesimal berkaitan dengan prinsip biner!
Contoh soal, ubahlah bilangan biner 101101011011001011 menjadi bilangan heks! (Lihat hasilnya pada Gambar 5 di bawah ini).
 |
| Gambar 5 |
Tabel Digit Oktal
| Digit Oktal | Ekivalens 3-Bit |
|---|---|
| 0 | 000 |
| 1 | 001 |
| 2 | 010 |
| 3 | 011 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
Tabel Digit Heksadesimal
| Digit Desimal | Ekivalens 4-Bit |
|---|---|
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
| A (10) | 1010 |
| B (11) | 1011 |
| C (12) | 1100 |
| D (13) | 1101 |
| E (14) | 1110 |
| F (15) | 1111 |
Demikianlah informasi mengenai tentang bagaimana Mengenal Konsep Bilangan Biner dan Desimal dalam Sistem Digital, semoga dapat bermanfaat.
Terima Kasih.

Post a Comment